知识专区

目录
零、算法概述
一、插入排序
二、冒泡排序
三、选择排序
四、计数排序
五、基数排序
六、归并排序
七、快速排序
八、随机快速
九、 希尔排序
十、 堆堆排序
今天的内容,将围绕这几张动图来展开。可以大致先简单看一下,这是一个归并排序的动图演示,我会对以上几个排序从 算法原理、动图详解 讲到 C语言 的 源码分析。

零、算法概述 今天要讲的内容是 「 十大排序算法 」。各个排序算法中的思想都非常经典,如果能够一一消化,那么在学习算法的路上也会轻松许多。
相信看我文章的大多数都是「 大学生 」,能上大学的都是「 精英 」,那么我们自然要「 精益求精 」,如果你还是「 大一 」,那么太好了,你拥有大把时间,没错!利用这个时间 「 学好算法 」,三年后的你自然「 不能同日而语 」。
🔥让天下没有难学的算法🔥
那么这里,我整理了「 几十个基础算法 」 的分类,有需要可以找我领取。大致一览:
C语言免费动漫教程,和我一起打卡! 🌞《光天化日学C语言》🌞
入门级C语言真题汇总 🧡《C语言入门100例》🧡
几张动图学会一种数据结构 🌳《画解数据结构》🌳
组团学习,抱团生长 🌌《算法入门指引》🌌
竞赛选手金典图文教程 💜《夜深人静写算法》💜
一、插入排序 「 插入排序 」 是比较好理解且编码相对简单的排序算法,虽然效率不是很高。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
通过不断将当前元素 「插入」 到 「升序」 序列中,直到所有元素都执行过 「插入」 操作,则算法结束。
3、命名由来
每次都是将元素 「插入」 到 有序 序列中,故此命名 「 插入排序 」 。
1、样例
| 8 | 5 | 6 | 4 | 3 | 7 | 10 | 2 |
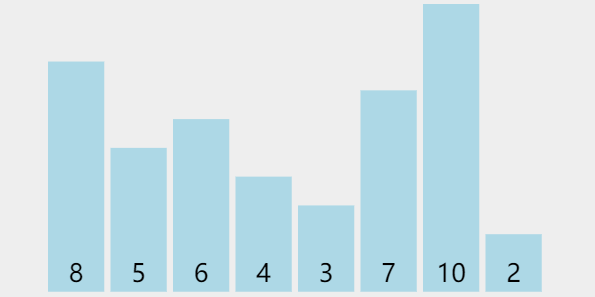
2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行 比较 和 移动 的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| ■ 的柱形 | 代表待执行插入的数 |
我们看到,首先需要将 「第二个元素」 和 「第一个元素」 进行 「比较」,如果 前者 小于等于 后者,则将 后者 进行向后 「移动」,前者 则执行插入;
然后,进行第二轮「比较」,即 「第三个元素」 和 「第二个元素」、「第一个元素」 进行 「比较」, 直到 「前三个元素」 保持有序 。
最后,经过一定轮次的「比较」 和 「移动」之后,一定可以保证所有元素都是 「升序」 排列的。
1、循环的实现
int n = 520; for(int i = 0; i < n; ++i) { // TODO : 。。。 }
2、比较的实现
#define Type int bool smallerEqualThan(Type a, Type b) { return a <= b; }
3、移动的实现
a[j + 1] = a[j];
1、问题描述
给定一个 n n n 个元素的数组,数组下标从 0 0 0 开始,采用「 插入排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程分以下几步:
1) 循环迭代变量 i = 1 → n − 1 i = 1 \to n-1 i=1→n−1;
2) 每次迭代,令 x = a [ i ] x = a[i] x=a[i], j = i − 1 j = i-1 j=i−1,循环执行比较 x x x 和 a [ j ] a[j] a[j],如果产生 x ≤ a [ j ] x \le a[j] x≤a[j] 则执行 a [ j + 1 ] = a [ j ] a[j+1] = a[j] a[j+1]=a[j]。然后执行 j = j + 1 j = j + 1 j=j+1,继续执行 2);否则,跳出循环,回到 1)。
1、时间复杂度
外循环正好运行 n − 1 n-1 n−1 次迭代。 但内部循环运行变得越来越短:
当 i = 1 i = 1 i=1,内层循环 1 1 1 次「比较」操作。
当 i = 2 i = 2 i=2,内层循环 2 2 2 次「比较」操作。
当 i = 3 i = 3 i=3,内层循环 3 3 3 次「比较」操作。
……
当 i = n − 2 i = n-2 i=n−2,内层循环 n − 2 n-2 n−2 次「比较」操作。
当 i = n − 1 i = n-1 i=n−1,内层循环 n − 1 n-1 n−1 次「比较」操作。
2、空间复杂度
「 插入排序 」在众多排序算法中效率较低,时间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
想象一下,当有 n = 1 0 5 n = 10^5 n=105 个数字。 即使我们的计算机速度超快,并且可以在 1 秒内计算 1 0 8 10^8 108 次操作,但冒泡排序仍需要大约一百秒才能完成。
考虑,在进行插入操作之前,我们找位置的过程是在有序数组中找的,所以可以利用「二分查找」 来找到对应的位置。然而,执行 「 插入 」 的过程还是 O ( n ) O(n) O(n),所以优化的也只是常数时间,最坏时间复杂度是不变的。
#include <stdio.h>
int a[1010];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i) printf(" "); printf("%d", a[i]); } puts(""); }
void InsertSort(int n, int *a) { // (1)
int i, j;
for(i = 1; i < n; ++i) { int x = a[i]; // (2)
for(j = i-1; j >= 0; --j) { // (3)
if(x <= a[j]) { // (4)
a[j+1] = a[j]; // (5)
}else break; // (6)
}
a[j+1] = x; // (7)
} }
int main() { int n; while(scanf("%d", &n) != EOF) { Input(n, a); InsertSort(n, a); Output(n, a); } return 0; }
二、冒泡排序 想要养成 「算法思维」,每一个简单的问题都要思考它背后的真正含义,做到 举一反三,触类旁通。
「 冒泡排序 」 是最好理解且编码最简单的排序算法。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
通过不断比较相邻的元素,如果「左边的元素」 大于 「右边的元素」,则进行「交换」,直到所有相邻元素都保持升序,则算法结束。
3、命名由来
数值大的元素经过交换,不断到达数组的尾部,就像气泡,逐渐浮出水面一样,故此命名 「 冒泡排序 」 。
1、样例
| 8 | 5 | 6 | 4 | 3 | 7 | 10 | 2 |

2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行比较的两个数 |
| ■ 的柱形 | 代表已经排好序的数 |
我们看到,首先需要将 「第一个元素」 和 「第二个元素」 进行 「比较」,如果 前者 大于 后者,则进行 「交换」,然后再比较 「第二个元素」 和 「第三个元素」 ,以此类推,直到 「最大的那个元素」 被移动到 「最后的位置」 。
然后,进行第二轮「比较」,直到 「次大的那个元素」 被移动到 「倒数第二的位置」 。
最后,经过一定轮次的「比较」 和 「交换」之后,一定可以保证所有元素都是 「升序」 排列的。
1、循环的实现
int n = 520; for(int i = 0; i < n; ++i) { // 循环体 }
2、比较的实现
#define Type int bool isBigger(Type a, Type b) { return a > b; }
3、交换的实现
a, b = b, a
当然是再找来一个临时杯子:
1)先把 a a a 杯子的水倒进这个临时的杯子里;
2)再把 b b b 杯子的水倒进 a a a 杯子里;
3)最后把临时杯子里的水倒进 b b b 杯子;
#define Type int void swap(Type* a, Type* b)
{ Type tmp = *a; // 把 a 杯子的水倒进临时杯子
*a = *b; // 把 b 杯子的水倒进 a 杯子
*b = tmp; // 把 临时杯子 的水 倒进 b 杯子 }
1、问题描述
给定一个 n n n 个元素的数组,数组下标从 0 0 0 开始,采用「 冒泡排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程分以下几步:
1) 循环迭代变量 i = 0 → n − 1 i = 0 \to n-1 i=0→n−1;
2) 每次迭代,令 j = i j = i j=i,循环执行比较 a [ j ] a[j] a[j] 和 a [ j + 1 ] a[j+1] a[j+1],如果产生 a [ j ] > a [ j + 1 ] a[j] \gt a[j+1] a[j]>a[j+1] 则交换两者的值。然后执行 j = j + 1 j = j + 1 j=j+1,这时候对 j j j 进行判断,如果 j ≥ n − 1 j \ge n-1 j≥n−1,则回到 1),否则继续执行 2)。
1、时间复杂度
外循环正好运行 n − 1 n-1 n−1 次迭代。 但内部循环运行变得越来越短:
当 i = 0 i = 0 i=0,内层循环 n − 1 n-1 n−1 次「比较」操作。
当 i = 1 i = 1 i=1,内层循环 n − 2 n-2 n−2 次「比较」操作。
当 i = 2 i = 2 i=2,内层循环 n − 3 n-3 n−3 次「比较」操作。
……
当 i = n − 2 i = n-2 i=n−2,内层循环 1 1 1 次「比较」操作。
当 i = n − 1 i = n-1 i=n−1,内层循环 0 0 0 次「比较」操作。
2、空间复杂度
「 冒泡排序 」在众多排序算法中效率较低,时间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
想象一下,当有 n = 1 0 5 n = 10^5 n=105 个数字。 即使我们的计算机速度超快,并且可以在 1 秒内计算 1 0 8 10^8 108 次操作,但冒泡排序仍需要大约一百秒才能完成。
但是,它的外层循环是可以提前终止的,例如,假设一开始所有数字都是升序的,那么在首轮「比较」的时候没有发生任何的「交换」,那么后面也就不需要继续进行 「比较」 了,直接跳出外层循环,算法提前终止。
#include <stdio.h>
int a[1010];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) {
scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i) printf(" "); printf("%d", a[i]); }
puts(""); } void Swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; }
void BubbleSort(int n, int *a) { // (1)
bool swapped; int last = n; do { swapped = false; // (2)
for(int i = 0; i < last - 1; ++i) { // (3)
if(a[i] > a[i+1]) { // (4)
Swap(&a[i], &a[i+1]); // (5)
swapped = true; // (6)
} }
--last; }
while (swapped); }
int main() { int n; while(scanf("%d", &n) != EOF) { Input(n, a); BubbleSort(n, a); Output(n, a); } return 0; }
三、选择排序
「 选择排序 」 是比较直观且编码简单的排序算法,虽然效率不是很高,但一般也出现在各种 「数据结构」 的教科书上。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
通过不断从未排序的元素中,「比较」 和 「交换」,从而 「选择」 出一个最小的, 直到最后变成一个「升序」 序列,则算法结束。
3、命名由来
每次都是「选择」 出一个最小的元素,故此命名 「 选择排序 」 。
1、样例
| 8 | 5 | 6 | 4 | 3 | 7 | 10 | 2 |

2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表正在执行 比较 的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| ■ 的柱形 | 有两种:1、记录最小元素 2、执行交换的元素 |
我们发现,首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第一个元素」 进行 「交换」;
然后,从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第二个元素」 进行 「交换」。
最后,一定可以保证所有元素都是 「升序」 排列的。
1、循环的实现
int n = 5201314; for(int i = 0; i < n; ++i) { // TODO : 。。。 }
2、比较的实现
#define Type int bool smallerThan(Type a, Type b) { return a < b; }
3、交换的实现
a, b = b, a
当然是再找来一个临时杯子:
1)先把 a a a 杯子的水倒进这个临时的杯子里;
2)再把 b b b 杯子的水倒进 a a a 杯子里;
3)最后把临时杯子里的水倒进 b b b 杯子;
#define Type
int void swap(Type* a, Type* b) {
Type tmp = *a; // 把 a 杯子的水倒进临时杯子
*a = *b; // 把 b 杯子的水倒进 a 杯子
*b = tmp; // 把 临时杯子 的水 倒进 b 杯子 }
1、问题描述
给定一个 n n n 个元素的数组,数组下标从 0 0 0 开始,采用「 选择排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程分以下几步:
1) 循环迭代变量 i = 0 → n − 1 i = 0 \to n-1 i=0→n−1;
2) 每次迭代,令 m i n = i min = i min=i, j = i + 1 j = i+1 j=i+1;
3) 循环执行比较 a [ j ] a[j] a[j] 和 a [ m i n ] a[min] a[min],如果产生 a [ j ] < a [ m i n ] a[j] \lt a[min] a[j]<a[min] 则执行 m i n = j min = j min=j。执行 j = j + 1 j = j + 1 j=j+1,继续执行这一步,直到 j = = n j == n j==n;
4) 交换 a [ i ] a[i] a[i] 和 a [ m i n ] a[min] a[min],回到 1)。
1、时间复杂度
外循环正好运行 n − 1 n-1 n−1 次迭代。 但内部循环运行变得越来越短:
当 i = 0 i = 0 i=0,内层循环 n − 1 n-1 n−1 次「比较」操作。
当 i = 1 i = 1 i=1,内层循环 n − 2 n-2 n−2 次「比较」操作。
当 i = 2 i = 2 i=2,内层循环 n − 3 n-3 n−3 次「比较」操作。
……
当 i = n − 3 i = n-3 i=n−3,内层循环 2 2 2 次「比较」操作。
当 i = n − 2 i = n-2 i=n−2,内层循环 1 1 1 次「比较」操作。
2、空间复杂度
「 选择排序 」在众多排序算法中效率较低,时间复杂度为 O ( n 2 ) O(n^2) O(n2) 。
想象一下,当有 n = 1 0 5 n = 10^5 n=105 个数字。 即使我们的计算机速度超快,并且可以在 1 秒内计算 1 0 8 10^8 108 次操作,但冒泡排序仍需要大约一百秒才能完成。
考虑一下,每一个内层循环是从一个区间中找到一个最小值,并且更新这个最小值。是一个「 动态区间最值 」问题,所以这一步,我们是可以通过「 线段树 」 来优化的。这样就能将内层循环的时间复杂度优化成 O ( l o g 2 n ) O(log_2n) O(log2n) 了,总的时间复杂度就变成了 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。
由于「 线段树 」不是本文讨论的重点,有兴趣了解「 线段树 」相关内容的读者,可以参考以下这篇文章:夜深人静写算法(三十九)- 线段树。
#include <stdio.h>
int a[1010];
void Input(int n, int *a) { for(int i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a) { for(int i = 0; i < n; ++i)
{ if(i) printf(" "); printf("%d", a[i]); } puts(""); } void Swap(int *a, int *b)
{ int tmp = *a; *a = *b; *b = tmp; } void SelectionSort(int n, int *a) { // (1)
int i, j;
for(i = 0; i < n - 1; ++i) { // (2)
int min = i; // (3)
for(j = i+1; j < n; ++j) { // (4)
if(a[j] < a[min]) { min = j; // (5)
} } Swap(&a[i], &a[min]); // (6)
} }
int main()
{ int n; while(scanf("%d", &n) != EOF)
{ Input(n, a); SelectionSort(n, a); Output(n, a); } return 0; }
四、计数排序 「 计数排序 」 是比较好理解且编码相对简单的排序算法,可以说是效率最高的排序算法之一,但是也有 「 局限性 」,这个后面我会讲。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
首先,准备一个 「 计数器数组 」,通过一次 「 枚举 」,对所有「 原数组 」元素进行计数。
然后,「 从小到大 」枚举所有数,按照 「 计数器数组 」 内的个数,将枚举到的数放回 「 原数组 」。执行完毕以后,所有元素必定按照 「升序」 排列。
3、命名由来
整个过程的核心,就是在 「计算某个数的数量」,故此命名 「 计数排序 」 。
1、样例
| 2 | 3 | 1 | 3 | 2 | 1 | 4 | 2 | 4 | 6 | 2 |

2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 计数为 0 的数 |
| ■ 的柱形 | 计数为 1 的数 |
| ■ 的柱形 | 计数为 2 的数 |
| ■ 的柱形 | 计数为 3 的数 |
| ■ 的柱形 | 计数为 4 的数 |
我们看到,首先程序生成了一个区间范围为 [ 1 , 9 ] [1, 9] [1,9] 的 「 计数器数组 」,并且一开始所有值的计数都为 0。
然后,遍历枚举「 原数组 」的所有元素,在 元素值 对应的计数器上执行 「 计数 」 操作。
最后,遍历枚举「 计数器数组 」,按照数组中元素个数放回到 「 原数组 」 中。这样,一定可以保证所有元素都是 「升序」 排列的。
1、循环的实现
int n = 111; for(int i = 0; i < n; ++i) { // TODO : 。。。 }
2、哈希的实现
cnt[5] = 1;
3、计数的实现
++cnt[5];
1、问题描述
给定一个 n n n 个元素的整型数组,数组下标从 0 0 0 开始,且数组元素范围为 [ 1 , 1 0 5 ] [1, 10^5] [1,105],采用「 计数排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程分以下几步:
1) 初始化计数器数组cnt[i] = 0,其中 i ∈ [ 1 , 1 0 5 ] i \in [1, 10^5] i∈[1,105];
2) 令 i = 0 → n − 1 i = 0 \to n-1 i=0→n−1,循环执行计数器数组的自增操作++cnt[a[i]];
3) 令 i = 1 → 100000 i = 1 \to 100000 i=1→100000,检测cnt[i]的值,如果非零,则将cnt[i]个i的值依次放入原数组a[]中。
1、时间复杂度
除了输入输出以外,「 计数排序 」 中总共有四个循环。
第一个循环,用于初始化 「 计数器数组 」,时间复杂度 O ( k ) O(k) O(k);
第二个循环,枚举所有数字,执行「 哈希 」 和 「 计数 」 操作,时间复杂度 O ( n ) O(n) O(n);
第三个循环,枚举所有范围内的数字,时间复杂度 O ( k ) O(k) O(k);
第四个循环,是嵌套在第三个循环内的,最多走 O ( n ) O(n) O(n),虽然是嵌套,但是它可第三个循环是相加的关系,而并非相乘的关系。
2、空间复杂度
「 计数排序 」在众多排序算法中效率最高,时间复杂度为 O ( n + k ) O(n + k) O(n+k) 。
但是,它的缺陷就是非常依赖它的数据范围。必须为整数,且限定在 [ 1 , k ] [1, k] [1,k] 范围内,所以由于内存限制, k k k 就不能过大,优化点都是常数优化了,主要有两个:
(1) 初始化 「 计数器数组 」 可以采用系统函数memset,纯内存操作,由于循环;
(2) 上文提到的第三个循环,当排序元素达到 n n n 个时,可以提前结束,跳出循环。
#include <stdio.h>
#include <string.h>
#define maxn 1000001
#define maxk 100001
int a[maxn];
int cnt[maxk];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) {
scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i) printf(" "); printf("%d", a[i]);
} puts(""); }
void CountingSort(int n, int *a) { // (1)
int i, top;
memset(cnt, 0, sizeof(cnt)); // (2)
for(i = 0; i < n; ++i) { // (3)
++cnt[ a[i] ]; // (4)
} top = 0; // (5)
for(i = 0; i < maxk; ++i) { while(cnt[i]) { // (6)
a[top++] = i; // (7)
--cnt[i]; // (8)
} if(top == n) { // (9)
break; } } }
int main() { int n; while(scanf("%d", &n) != EOF)
{ Input(n, a); CountingSort(n, a); Output(n, a); } return 0; }
五、基数排序 「 基数排序 」 很好的弥补了 「 计数排序 」 中待排序的数据范围过大的问题,它适合 「 范围大 」 且 「 数位少 」 的整数的排序。它将所有的整数认为是一个字符串,从最低有效位(最右边的)到 最高有效位(最左边的)开始迭代。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
首先,准备 10 个队列,进行若干次「 迭代 」。每次「 迭代 」,先清空队列,然后取每个待排序数的对应十进制位,通过「 哈希 」,映射到它「 对应的队列 」中,然后将所有数字「 按照队列顺序 」塞回「 原数组 」完成一次「 迭代 」。
可以认为类似「 关键字排序 」,先对「 第一关键字 」进行排序,再对「 第二关键字 」排序,以此类推,直到所有关键字都有序为止。
1、样例
| 3121 | 897 | 3122 | 3 | 23 | 5 | 55 | 7 | 97 | 123 | 456 | 1327 |

2、算法演示

3、样例说明
我们看到,首先程序生成了一个区间范围为 [ 0 , 9 ] [0, 9] [0,9] 的 「 基数队列 」。
然后,总共进行了 4 轮「 迭代 」(因为最大的数总共 4 个数位)。
每次迭代,遍历枚举 「 原数组 」 中的所有数,并且取得本次迭代对应位的数字,通过「 哈希 」,映射到它「 对应的队列 」中 。然后将 「 队列 」 中的数据按顺序塞回 「 原数组 」 完成一次「 迭代 」,4 次「 迭代 」后,一定可以保证所有元素都是 「升序」 排列的。
1、循环的实现
int n = 128; for(int i = 0; i < n; ++i) { // TODO : 。。。 }
2、哈希的实现
cnt[5] = 1;
3、队列的实现
4、十进制位数计算
1、问题描述
给定一个 n n n 个元素的整型数组,数组下标从 0 0 0 开始,且数组元素范围为 [ 1 , 1 0 8 ) [1, 10^8) [1,108),采用「 基数排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程分以下几步:
1) 定好进制,一般为 10 10 10,然后预处理 10 10 10 的幂,存储在数组中,PowOfBase[i]代表 1 0 i 10^i 10i;
2) 由于数据范围为 [ 1 , 99999999 ] [1, 99999999] [1,99999999],即 8 8 8 个 9 9 9,最多 8 8 8 位,所以可以令 p o s = 0 → 7 pos = 0 \to 7 pos=0→7,执行下一步;
3) 初始化 [ 0 , 9 ] [0,9] [0,9] 队列,对 n n n 个数字取 p o s pos pos 位,放入对应的队列中;
4) 从第 0 0 0 个队列到 第 9 9 9 个队列,将所有数字按照顺序取出来,放回原数组,然后 p o s = p o s + 1 pos = pos + 1 pos=pos+1,回到 3) 继续迭代;
1、时间复杂度
除了输入输出以外,「 基数排序 」 中总共有 k k k 轮 「 迭代 」。
每一轮「 迭代 」,都需要遍历数组中的所有数,进行 「 入队 」 操作,时间复杂度 O ( n ) O(n) O(n)。所有数都 「 入队 」 完毕以后,需要将所有队列中的数塞回 「 原数组 」 ,时间复杂度也是 O ( n ) O(n) O(n)。
2、空间复杂度
「 基数排序 」 的时间复杂度为 O ( n k ) O(nk) O(nk) 。
其中 k k k 代表数字位的个数,所以比较依赖数据,如果最大的那个数的位数小,某次迭代下来,所有的数都已经放在一个队列中了,那就没必要继续迭代了。这里可以进行一波常数优化。
#include <stdio.h>
#include <string.h>
const int MAXN = 100005; // (1)
const int MAXT = 8; // (2)
const int BASE = 10; // (3)
int PowOfBase[MAXT]; // (4)
int RadixBucket[BASE][MAXN]; // (5)
int RadixBucketTop[BASE]; // (6)
void InitPowOfBase() { int i;
PowOfBase[0] = 1;
for(i = 1; i < MAXT; ++i) {
PowOfBase[i] = PowOfBase[i-1] * BASE; // (7)
} } void Input(int n, int *a) {
int i; for(i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a)
{ int i; for(i = 0; i < n; ++i) { if(i) printf(" ");
printf("%d", a[i]); } puts(""); }
int getRadix(int value, int pos) { return value / PowOfBase[pos] % BASE; // (8)
} void RadixSort(int n, int *a) { // (9)
int i, j, top = 0, pos = 0;
while (pos < MAXT) { // (10)
memset(RadixBucketTop, 0, sizeof(RadixBucketTop)); // (11)
for(i = 0; i < n; ++i) { int rdx = getRadix(a[i], pos);
RadixBucket[ rdx ][ RadixBucketTop[rdx]++ ] = a[i]; // (12)
} top = 0; for(i = 0; i < BASE; ++i)
{ for(j = 0; j < RadixBucketTop[i]; ++j) {
a[top++] = RadixBucket[i][j]; // (13)
} } ++pos;
} }
int a[MAXN];
int main() {
int n; InitPowOfBase();
while(scanf("%d", &n) != EOF) {
Input(n, a); RadixSort(n, a); Output(n, a); } return 0; }
/*
15
3221 1 10 9680 577 9420 7 5622 4793 2030 3138 82 2599 743 4127
*/
六、归并排序 「 归并排序 」 是利用了 「分而治之 」 的思想,进行递归计算的排序算法,效率在众多排序算法中的佼佼者,一般也会出现在各种 「数据结构」 的教科书上。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
通过将当前乱序数组分成长度近似的两份,分别进行「 递归 」 调用,然后再对这两个排好序的数组,利用两个指针,将数据元素依次比较,选择相对较小的元素存到一个「 辅助数组 」中,再将「 辅助数组 」中的数据存回「 原数组 」。
3、命名由来
每次都是将数列分成两份,分别排序后再进行 「 归并 」,故此命名 「 归并排序 」 。
1、样例
| 8 | 5 | 6 | 4 | 3 | 7 | 10 | 2 |

2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表已经排好序的数 |
| 其他颜色 ■ 的柱形 | 正在递归、归并中的数 |
我们发现,首先将 「 8个元素 」 分成 「 4个元素 」,再将 「 4个元素 」 分成 「 2个元素 」,然后 「比较」这「 2个元素 」的值,使其在自己的原地数组内有序,然后两个 「 2个元素 」 的数组归并变成 「 4个元素 」 的 「升序」数组,再将两个「 4个元素 」 的数组归并变成 「 8个元素 」 的 「升序」数组。
1、递归的实现
int sum(int n) { if(n <= 0) { return 0; } return sum(n - 1) + n; }
2、比较的实现
#define Type int bool smallerThan(Type a, Type b) { return a < b; }
3、归并的实现
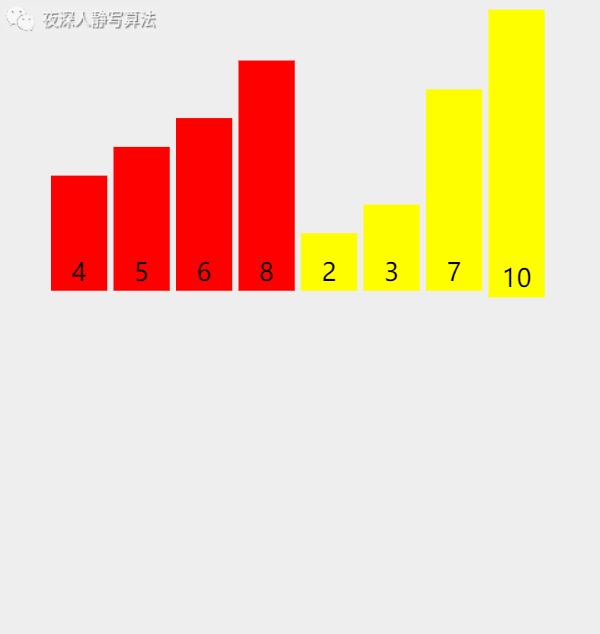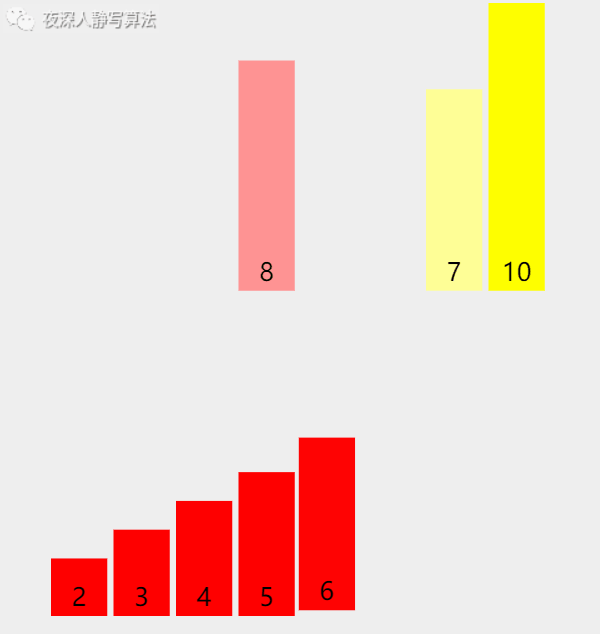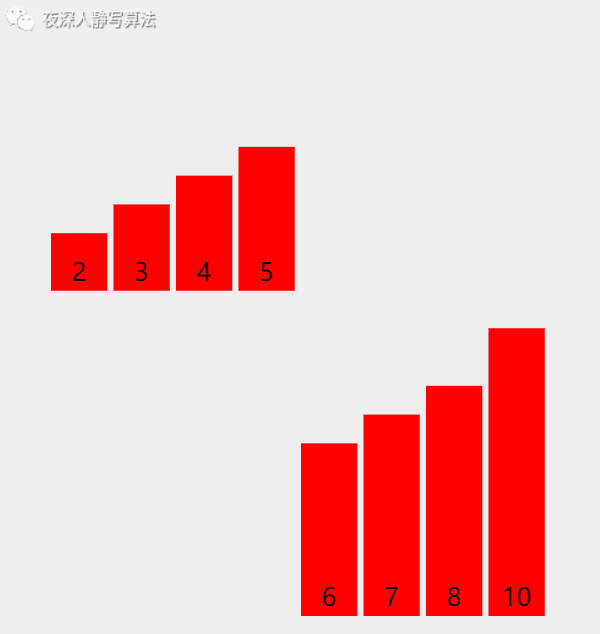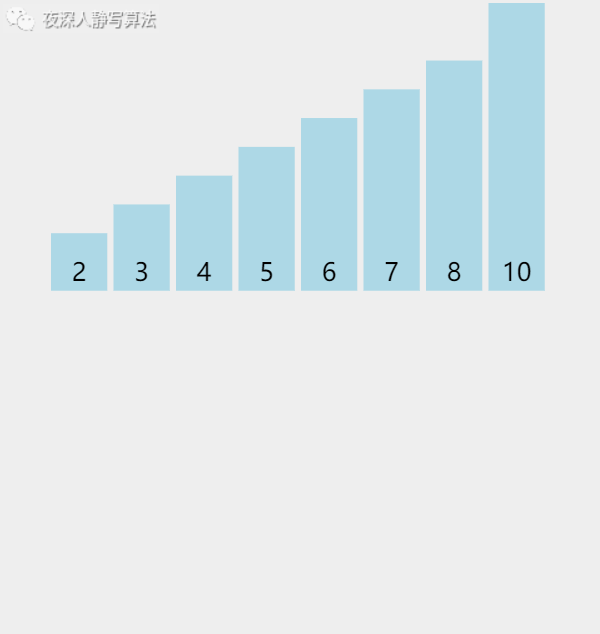
1、问题描述
给定一个 n n n 个元素的数组,数组下标从 0 0 0 开始,采用「 归并排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程用mergeSort(a[], l, r)描述,代表 当前待排序数组 a a a,左区间下标 l l l,右区间下标 r r r,分以下几步:
1) 计算中点 m i d = l + r 2 mid = \frac {l + r}{2} mid=2l+r;
2) 递归调用mergeSort(a[], l, mid)和mergeSort(a[], mid+1, r);
3) 将 2)中两个有序数组进行有序合并,再存储到a[l:r];
4) 调用时,调用mergeSort(a[], 0, n-1)就能得到整个数组的排序结果。
「 递归 」是自顶向下的,实际上程序真正运行过程是自底向上「 回溯 」的过程:给定一个 n
n n 个元素的数组,「 归并排序 」 将执行如下几步:
1)将每对单个元素归并为 2个元素 的有序数组;
2)将 2个元素 的每对有序数组归并成 4个元素 的有序数组,重复这个过程…;
3)最后一步:归并 2 个 n
/
2
n / 2 n/2 个元素的排序数组(为了简化讨论,假设 n
n n 是偶数)以获得完全排序的 n
n n 个元素数组。
1、时间复杂度
2、空间复杂度
「 归并排序 」在众多排序算法中效率较高,时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n) 。
但是,由于归并排序在归并过程中需要额外的一个「 辅助数组 」,所以申请「 辅助数组 」内存空间带来的时间消耗会比较大,比较好的做法是,实现用一个和给定元素个数一样大的数组,作为函数传参传进去,所有的 「 辅助数组 」 干的事情,都可以在这个传参进去的数组上进行操作,这样就免去了内存的频繁申请和释放。
#include <stdio.h>
#include <malloc.h>
#define maxn 1000001
int a[maxn];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) { if(i) printf(" ");
printf("%d", a[i]); } puts(""); }
void MergeSort(int *nums, int l, int r) {
int i, mid, p, lp, rp; int *tmp = (int *)malloc( (r-l+1) * sizeof(int) ); // (1)
if(l >= r) { return ; // (2)
} mid = (l + r) >> 1; // (3)
MergeSort(nums, l, mid); // (4)
MergeSort(nums, mid+1, r); // (5)
p = 0; // (6)
lp = l, rp = mid+1; // (7)
while(lp <= mid || rp <= r) { // (8)
if(lp > mid) { tmp[p++] = nums[rp++]; // (9)
}else if(rp > r) { tmp[p++] = nums[lp++]; // (10)
}else { if(nums[lp] <= nums[rp]) { // (11)
tmp[p++] = nums[lp++]; }else { tmp[p++] = nums[rp++]; } } }
for(i = 0; i < r-l+1; ++i) { nums[l+i] = tmp[i]; // (12)
} free(tmp); // (13)
} int main() { int n; while(scanf("%d", &n) != EOF) { Input(n, a); MergeSort(a, 0, n-1); Output(n, a); } return 0; }
七、快速排序 「 快速排序 」 是利用了 「分而治之 」 的思想,进行递归计算的排序算法,效率在众多排序算法中的佼佼者。
1、算法目的
将原本乱序的数组变成有序,可以是 「升序」 或者 「降序」 (为了描述统一,本文一律只讨论 「 升序」 的情况)。
2、算法思想
随机找到一个位置,将比它小的数都放到它 「 左边 」,比它大的数都放到它「 右边 」,然后分别「 递归 」求解 「 左边 」和「 右边 」使得两边分别有序。
3、命名由来
由于排序速度较快,故此命名 「 快速排序 」 。
1、样例
| 8 | 5 | 6 | 4 | 3 | 7 | 10 | 2 |

2、算法演示

3、样例说明
| 图示 | 含义 |
|---|---|
| ■ 的柱形 | 代表尚未排好序的数 |
| ■ 的柱形 | 代表随机选定的基准数 |
| ■ 的柱形 | 代表已经排序好的数 |
| ■ 的柱形 | 代表正在遍历比较的数 |
| ■ 的柱形 | 代表比基准数小的数 |
| ■ 的柱形 | 代表比基准数大的数 |
我们发现,首先随机选择了一个 7 作为「 基准数 」,并且将它和最左边的数交换。然后往后依次遍历判断,小于 7 的数为 「 绿色 」 ,大于 7 的数为「 紫色 」,遍历完毕以后,将 7 和 「 下标最大的那个比 7 小的数 」交换位置,至此,7的左边位置上的数都小于它,右边位置上的数都大于它,左边和右边的数继续递归求解即可。
1、递归的实现
int sum(int n) { if(n <= 0) { return 0; } return sum(n - 1) + n; }
2、比较的实现
#define Type int bool smallerThan(Type a, Type b) { return a < b; }
3、分治的实现

1、问题描述
给定一个 n n n 个元素的数组,数组下标从 0 0 0 开始,采用「 快速排序 」将数组按照 「升序」排列。
2、算法过程
整个算法的执行过程用quickSort(a[], l, r)描述,代表 当前待排序数组 a a a,左区间下标 l l l,右区间下标 r r r,分以下几步:
1) 随机生成基准点 p i v o x = P a r t i t i o n ( l , r ) pivox = Partition(l, r) pivox=Partition(l,r);
2) 递归调用quickSort(a[], l, pivox - 1)和quickSort(a[], pivox +1, r);
3) Partition(l, r)返回一个基准点,并且保证基准点左边的数都比它小,右边的数都比它大;Partition(l, r)称为分区。
1、时间复杂度
2、空间复杂度
「 快速排序 」在众多排序算法中效率较高,平均时间复杂度为 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)。但当完全有序时,最坏时间复杂度达到最坏情况 O ( n 2 ) O(n^2) O(n2)。
所以每次在选择基准数的时候,我们可以尝试用随机的方式选取,这就是 「 随机快速排序 」。
想象一下在随机化版本的快速排序中,随机化数据透视选择,我们不会总是得到 0 0 0, 1 1 1 和 n − 1 n-1 n−1 这种非常差的分割。所以不会出现上文提到的问题。
1、快速排序实现1
#include <stdio.h>
#include <malloc.h>
#define maxn 1000001
int a[maxn];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) { if(i) printf(" ");
printf("%d", a[i]); } puts(""); }
void Swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; }
int Partition(int a[], int l, int r){
int i, j, pivox; int idx = l + rand() % (r - l + 1); // (1)
pivox = a[idx]; // (2)
Swap(&a[l], &a[idx]); // (3)
i = j = l + 1; // (4) //
while( i <= r ) { // (5)
if(a[i] < pivox) { // (6)
Swap(&a[i], &a[j]); ++j; } ++i; // (7)
} Swap(&a[l], &a[j-1]); // (8)
return j-1; } //递归进行划分
void QuickSort(int a[], int l, int r){ if(l < r){
int mid = Partition(a, l, r); QuickSort(a, l, mid-1);
QuickSort(a, mid+1, r); } }
int main() { int n; while(scanf("%d", &n) != EOF) {
Input(n, a); QuickSort(a, 0, n-1); Output(n, a); } return 0; }
2、快速排序实现2
#include <stdio.h>
#include <malloc.h>
#define maxn 1000001
int a[maxn];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) { scanf("%d", &a[i]); } }
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i) printf(" "); printf("%d", a[i]); } puts(""); }
void Swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; }
int Partition(int a[], int l, int r){ int i, j; int idx = l + rand() % (r - l + 1); // (1)
Swap(&a[l], &a[idx]); // (2)
i = l, j = r; // (3)
int x = a[i]; // (4)
while(i < j){ while(i < j && a[j] > x) // (5)
j--; if(i < j) Swap(&a[i], &a[j]), ++i; // (6)
// while(i < j && a[i] < x) // (7)
i++; if(i < j) Swap(&a[i], &a[j]), --j; // (8)
} a[i] = x; return i; } //递归进行划分
void QuickSort(int a[], int l, int r){ if(l < r){ int mid = Partition(a, l, r);
QuickSort(a, l, mid-1); QuickSort(a, mid+1, r); } } int main() { int n; while(scanf("%d", &n) != EOF)
{ Input(n, a); QuickSort(a, 0, n-1); Output(n, a); } return 0; }
八、随机快速 「 随机快速排序 」 在上文已经有所介绍,即基准数的选择采用随机的方式进行。
九、 希尔排序 文章较长,导致编辑卡顿,故后续将在如下链接更新。 《画解数据结构》(4 - 8)- 希尔排序
十、 堆堆排序 文章较长,导致编辑卡顿,故后续将整理至在如下链接更新。 《画解数据结构》(2 - 3)- 堆 与 优先队列

